Wir vergleichen a[0] mit a[1]; wenn a[0] > a[1] ist, dann werden die beiden Zahlen ausgetauscht;Nun steht sicher in a[0] das kleinste der Elemente des Arrays. Jetzt suchen wir das zweitkleinste Element, d.h. das kleinste im Teilarray a[1..15]:
wir vergleichen a[0] mit a[2]; wenn a[0] > a[2] ist, dann werden die beiden Zahlen ausgetauscht;
wir vergleichen a[0] mit a[3]; wenn a[0] > a[3] ist, dann werden die beiden Zahlen ausgetauscht;
..... (usw bis) .....
wir vergleichen a[0] mit a[15]; wenn a[0] > a[15] ist, dann werden die beiden Zahlen ausgetauscht.
Wir vergleichen a[1] mit a[2]; wenn a[1] > a[2] ist, dann werden die beiden Zahlen ausgetauscht;Danach stimmen die ersten beiden Zahlen im (ganzen!) Array; wir können uns also der Sortierung des Teilarrays a[2..15] zuwenden, und dann a[3..15], a[4..15],..... bis schließlich a[14..15]. Dann ist das ganze Array sortiert.
wir vergleichen a[1] mit a[3]; wenn a[1] > a[3] ist, dann werden die beiden Zahlen ausgetauscht;
..... (usw bis) .....
wir vergleichen a[1] mit a[15]; wenn a[1] > a[15] ist, dann werden die beiden Zahlen ausgetauscht.
|
In Delphi stellen Sie dazu zunächst eine entsprechende Integer-Array-Variable zur Verfügung, die im ganzen Programm bekannt ist: deklarieren Sie sie daher im private-Abschnitt der Formular-Deklaration. Den Inhalt des Array können Sie dann mit Hilfe einer Prozedur (z.B. "ZeigeTabelle()") in einer StringGrid-Komponente darstellen lassen. Sorgen Sie beim Programmstart für eine entsprechende Beschriftung des StringGrid sowie für die Füllung des Arrays mit Zufallszahlen (zwischen 0 und 100) und deren Anzeige. Für die Details des Umganges mit der nicht ganz einfach zu handhabenden Komponente "StringGrid" sollten Sie die Delphi-Hilfe zu Rate ziehen. Nahezu alle relevanten Einstellungen lassen sich über die im Objekt-Inspektor aufgeführten Eigenschaften einstellen. Zur Implementierung des Sortierungsalgorithmus ist es sinnvoll, eine Prozedur "tausche()" zur Verfügung zu stellen, die zwei übergebene Integerzahlen vertauscht. Dabei gibt es 2 Möglichkeiten für die Parameter: entweder Sie übergeben direkt die Zahlen oder Sie übergeben nur die Indizes der Zahlen im Array. Welche der Möglichkeiten Sie wählen, hat einen gravierenden Einfluß auf die nötige Parameterliste der Prozedur! Warum? Außerdem ist es im Hinblick auf spätere Untersuchungen der verschiedenen Sortieralgorithmen sinnvoll, auch den Vergleich zweier Array-Einträge auszulagern, und zwar in eine boolsche Funktion "vergleiche()" (oder auch "istGroesser()"). Auch hier haben Sie wieder die beiden obengenannten Möglichkeiten für die Wahl des Parameter-Designs. Diesmal ist die Sache aber nicht so kritisch. Warum? |
In Java stellen Sie dazu zunächst eine entsprechende Integer-Array-Variable zur Verfügung, in der dann der eigentliche Sortiervorgang stattfinden wird. Diese Variable sollte auf derselben logischen Ebene deklariert werden wie die visuellen Komponenten Ihres Formulars, damit sie nämlich (genau wie diese) im gesamten Programm bekannt ist. Den Inhalt dieses Arrays können Sie dann mit Hilfe einer Prozedur (z.B. "moveIntsFromArrayToTable()" ) in einer Zeile einer jTable-Komponente darstellen lassen. Mit der Eigenschaft jTable.Columns können Sie schon zur Programmierzeit für passende Spaltenüberschriften sorgen: tragen Sie dort die Spalten-Nummern Zur Implementierung des Sortier-Algorithmus ist es sinnvoll, eine Prozedur "switchData()" zur Verfügung zu stellen, die zwei übergebene Integerzahlen vertauscht. Dabei ist es sinnvoll, dieser Prozedur die Array-Indizes der beiden zu vergleichenden Zahlen zu übergeben. Außerdem ist es im Hinblick auf spätere Untersuchungen der verschiedenen Sortieralgorithmen sinnvoll, auch den Vergleich zweier Array-Einträge auszulagern, und zwar in eine boolsche Funktion "compareData()", der ebenfalls die Array-Indizes der zu vergleichenden Daten übergeben werden. |
| v(16) | v(32) | v(160) | t(16) | t(32) | t(160) | |
|---|---|---|---|---|---|---|
| Austausch-Sort | 120 | 496 | 12720 | 49,2 | 218,6 | 5481,2 |
| Bubble-Sort | 120 | 496 | 12720 | 21,0 | 90,0 | 1951,6 |
| Auswahl-Sort | 120 | 496 | 12720 | 12,4 | 27,4 | 154,4 |
Die folgende Delphi-Prozedur läßt sich in jedem Programm einsetzen, das Sortieren soll; es muss dazu nur die zu sortierenden Daten in einem (linearen) Array "data" bereithalten und die boolsche Vergleichs-Funktion
procedure QuickSort;
procedure qs(li, re: Integer);
var i, j, v: Integer;
begin
i := li; j := re;
v := data[(li+re) Div 2];
Repeat
While IsLessThan(data[i], v) do
i := i + 1;
While IsLessThan(v, data[j]) do
j := j - 1;
If i <= j then begin
Exchange(data[i], data[j]);
i := i + 1;
j := j - 1;
end;
until i > j;
If li < j then qs(li, j);
If i < re then qs(i, re);
end;
begin
qs(0, Pred(max));
end;
Wenn Sie sich diesen Quelltext genauer anschauen, dann sehen Sie, dass er ganz schön raffiniert ist: die Prozedur "QuickSort" enthält eine lokale Prozedur "qs()", der zwei Integerwerte übergeben werden. Diese beschreiben den Index-Bereich des Arrays "data", in dem der aktuelle Aufruf von "qs" wirksam wird. Das Array "data" muss "max" Felder enthalten, die beginnend mit "0" durchnummeriert werden. Der erste Aufruf von "qs" geschieht in der Prozedur "QuickSort" selbst, und dort wird der gesamte Index-Bereich des "data"-Arrays übergeben. |
Die folgende Java-Prozedur läßt sich in jedem Programm einsetzen, das Sortieren soll; es muss dazu nur die zu sortierenden Daten in einem (linearen) Array "data" bereithalten und die boolsche Vergleichs-Funktion
public void QuickSort {
qs(0, Pred(max));
}
private void qs(int li, int re) {
int i = li;
int j = re;
int v = data[(li+re) / 2];
do {
while (isLessThan(data[i], v)) {
i = i + 1;
}
while (isLessThan(v, data[j])) {
j = j - 1;
}
if (i <= j) {
switchData(i, j);
i = i + 1;
j = j - 1;
}
} while (i ≤ j);
if (li < j) { qs(li, j) };
if (i < re) { qs(i, re) };
}
Wenn Sie sich diesen Quelltext genauer anschauen, dann sehen Sie, dass er ganz schön raffiniert ist: die Prozedur "QuickSort" ruft eine Prozedur "qs()" auf, der zwei Integerwerte übergeben werden. Diese beschreiben den Index-Bereich des Arrays "data", in dem der aktuelle Aufruf von "qs" wirksam wird. Das Array "data" muss "max" Felder enthalten, die beginnend mit "0" durchnummeriert werden. Beim ersten Aufruf von "qs" in der Prozedur "QuickSort" wird der gesamte Index-Bereich des "data"-Arrays übergeben. |
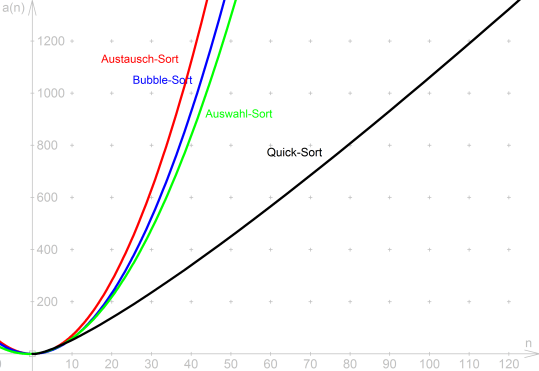
| Austausch-Sort | Bubble-Sort | Auswahl-Sort | Quick-Sort | |
|---|---|---|---|---|
| v(n) | 0,5*n² | 0,5*n² | 0,5*n² | 4,3*n*log(n) |
| t(n) | 0,2*n² | 0,08*n² | 0,9*n | 1,0*n*log(n) |
| a(n) | 0,7*n² | 0,58*n² | 0,5*n²+0,9*n | 5,3*n*log(n) |