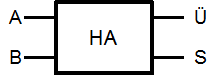
| A | B | Ü | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| Bits | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zahl | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
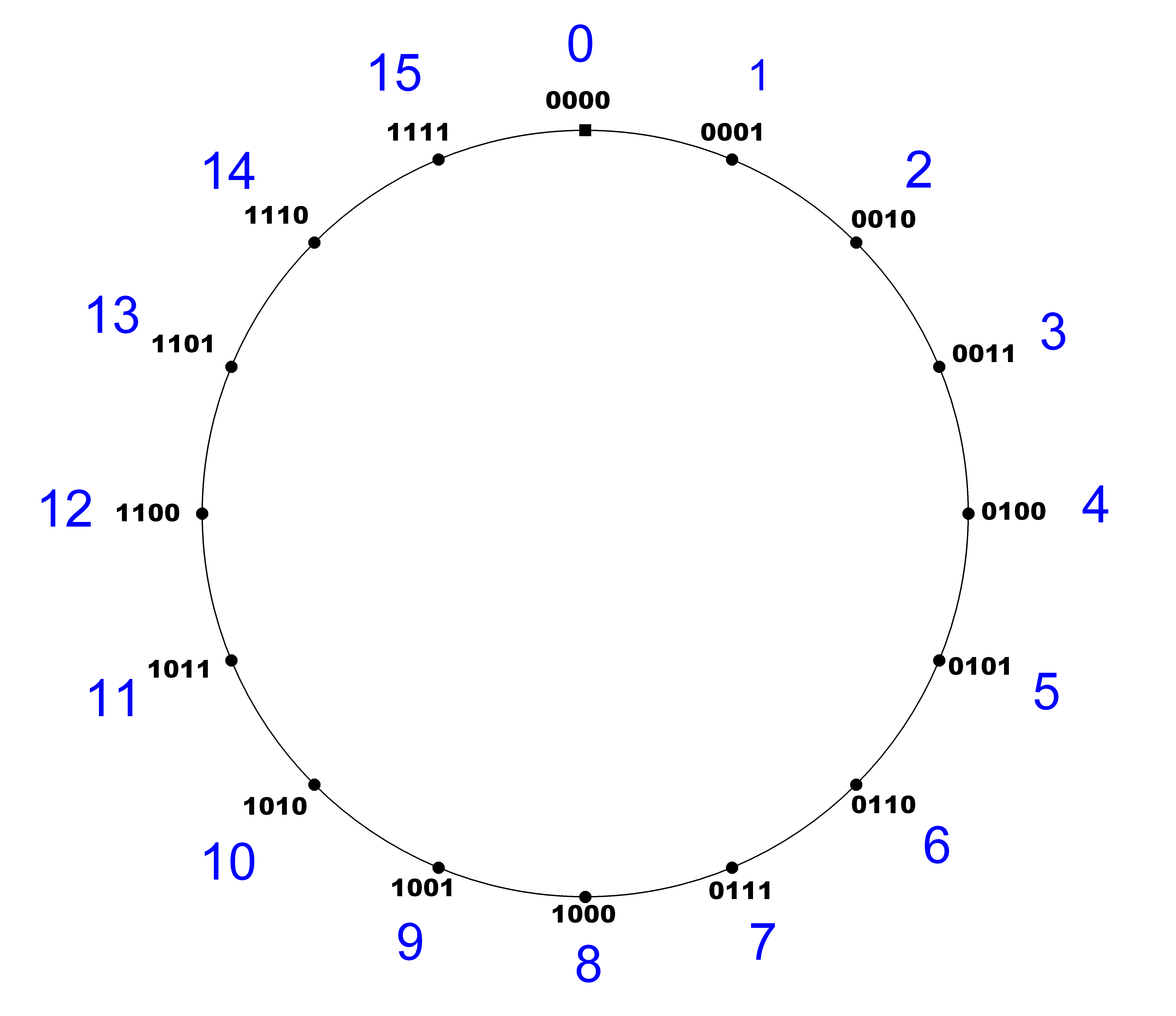
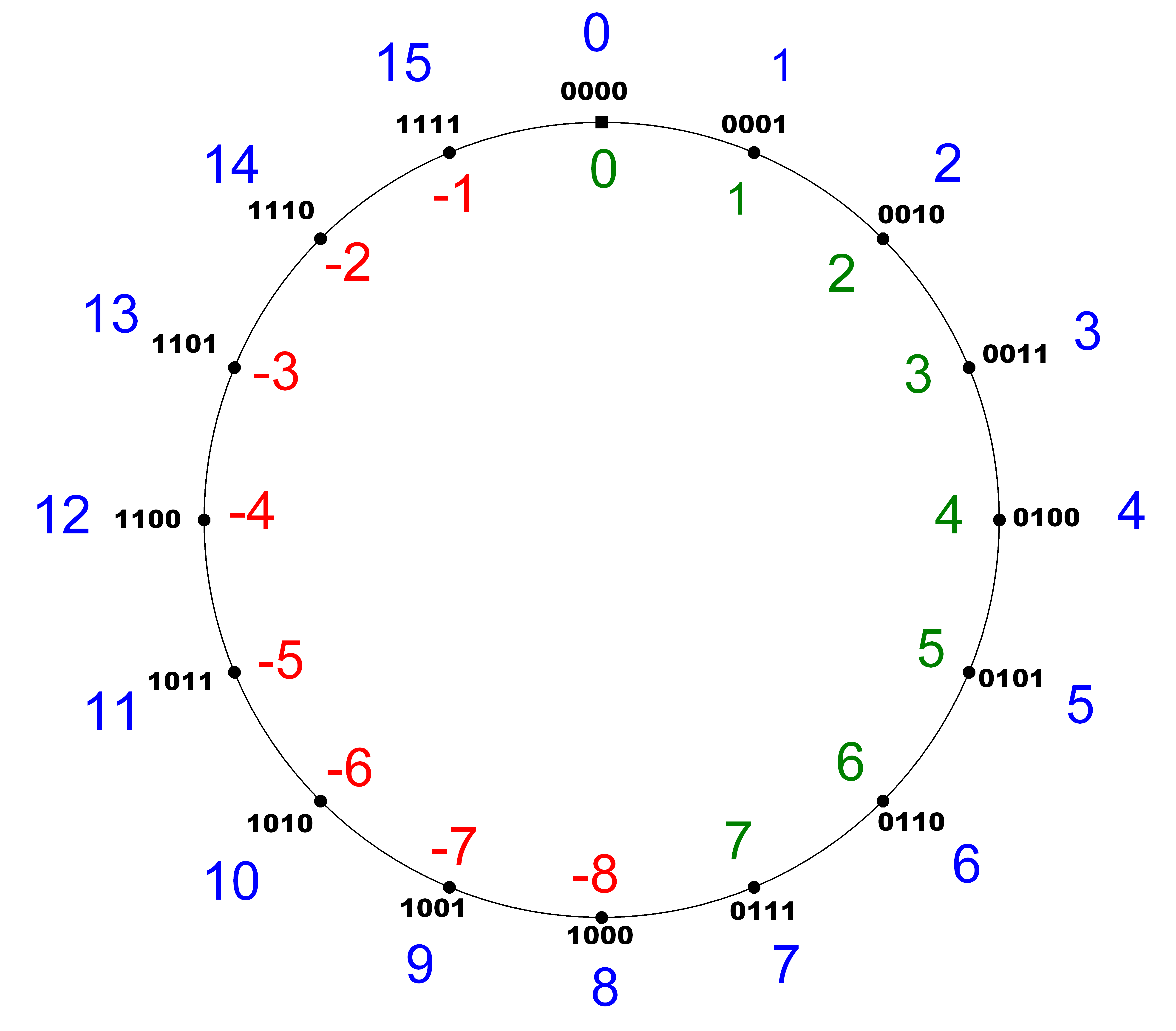
Man invertiere das Bitmuster von a und addiere zum Ergebnis eine 1.Wenn wir das bitweise Inverse einer Zahl a mit abi bezeichnen und das Zweier-Komplement von a mit a*, dann lässt sich die obige Regel als Formel schreiben:
a* = abi + 1Um den Nutzen der Zweierkomplement-Darstellung für negative Zahlen einzusehen, klären wir zunächst, wie man die Bildung des Zweierkomplements einer Zahl a mathematisch beschreiben kann. Liegt a in einer Darstellung mit N Bits vor, dann kann man das bitweise Inverse von a, also abi, erhalten, indem man a von einer Binärzahl abzieht, die aus genau N Einsen besteht. Im obigen konkreten Beispiel wäre also zu rechnen: "1111" - "0011" = "1100", wobei die Differenz in Zahlen geschrieben bedeutet: (24 – 1) – 3. Die Zweierkomplement-Darstellung erhält man nun, indem man zu diesem Term noch eine 1 addiert: (24 – 1) – 3 + 1 = 24 – 3. Allgemein ergibt sich für das Zweier-Komplement a* einer positiven Zahl a in N-stelliger Binärdarstellung der Term
a* = 2N – a.
b – a = b – a + 2N – 2N = b + 2N – a – 2N = b + (2N – a) – 2N = b + a* – 2NZur Ausführung der Subtraktion b - a kann also ein normales Addierwerk verwendet werden, wenn man an dessen Eingänge den Minuenden b und die Zweierkomplement-Darstellung a* des Subtrahenden anlegt und vom Ergebnis schließlich noch 2N abzieht. Die Subtraktion von 2N schließlich können wir einfach realisieren, indem wir ein eventuell gesetztes Übertrags-Bit in der höchstwertigen Stelle des Ergebnisses ignorieren: da dieses zusätzliche Bit ohnehin beim Abspeichern in einem N-Bit-Datenwort keinen Platz hat, lässt man es einfach unberücksichtigt.
b – a = b + (-a)die wir ja aus der Mathematik kennen. Für uns sieht diese Gleichung nun (bei Beschränkung auf N Binärstellen!) so aus:
b – a = b + a*.Wie aber erhält man aus dem Bitmuster einer Zahl a das Bitmuster der zugehörigen Zweier-Komplements a*? Dieses Problem haben wir bisher noch nicht wirklich gelöst: oben wird a* als Differenz dargestellt wird, nämlich a* = 2N - a. Also brauchen wir zur Berechnung von a* eine Subtrahier-Maschine, was schwierig wird, weil unser Addierer nur dann als Subtrahierer einsetzbar ist, wenn wir a* schon berechnen können!
|
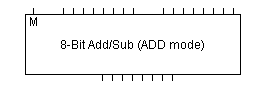
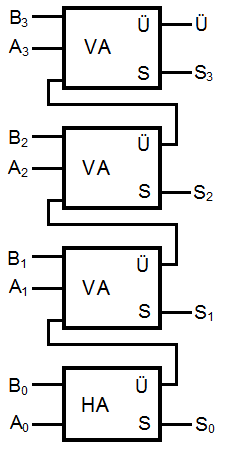
Die Implementierung ist sehr sparsam: für die Addition der 1 genügt eine 4er-Serie von Halbaddierern. Der unterste Input-Schalter wählt die Betriebsart: steht er auf "0", dann wird die links eingestellte Zahl b unverändert in die Ausgänge auf der rechten Seite weitergeleitet; steht er jedoch auf "1", dann erscheint rechts das Zweier-Komplement b* der links eingestellten Zahl b.