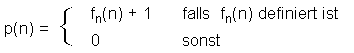2 Algorithmen als Funktionen

2.1 Was genau ist ein Algorithmus?
2.2 Wie viele Algorithmen gibt es?
2.3 Kann ein Computer "alles" berechnen?

Zum vorigen Kapitel Zum Inhaltsverzeichnis Zum nächsten Kapitel

2.1 Was genau ist ein Algorithmus?

 Wenn wir Computer-Programmen bei der Arbeit zusehen, dann fällt auf, dass alle dabei zu beobachtenden Algorithmen nach dem "E-V-A"-Prinzip arbeiten: ein Satz von Eingabedaten wird an den Algorithmus übergeben, dieser "bearbeitet" diese Daten und gibt dann einen Satz von Ausgabedaten zurück. Algorithmen verhalten sich also eigentlich genau wie Funktionen.

Allerdings können die Daten, mit denen Algorithmen zu tun haben, gelegentlich schon sehr komplizierte Strukturen aufweisen, und das macht eine weitere allgemeine Untersuchung recht schwierig. Die Tatsache aber, dass alle Daten, die ein Computer bearbeitet, stets in binärer Form vorliegen müssen, erlaubt uns, von den im realen Einzelfall vorliegenden Datentypen zu abstrahieren, und die Daten schlicht und ergreifend als (lange) natürliche Zahlen anzusehen! Damit kann man einen Algorithmus also durch eine Funktion darstellen, die eine Menge von natürlichen Zahlen als Argumente übergeben bekommt und danach eine (andere) Menge von natürlichen Zahlen-Werten zurückgibt.

Möglicherweise erscheint die Reduktion aller möglichen Datentypen auf natürliche Zahlen etwas gewaltsam. Man kann dies abmildern, indem man den Prozess zweistufig gestaltet: Zunächst sollen die Daten die Schnittstellen des Algorithmus nur in Textform passieren. Da sich alle Daten immer in Textform darstellen lassen, ist dies keine wesentliche Einschränkung. In einem zweiten Schritt codiert man diese Texte nun binär und interpretiert das erhaltene Bitmuster wieder als (eventuell sehr lange) natürliche Zahl. Diese Methode zeigt darüberhinaus, dass die Funktionen, welche die Algorithmen darstellen, eigentlich nur ein Argument benötigen, und ebenfalls nur eine Zahl als Ergebnis liefern müssen, ohne dass dies die Allgemeinheit unserer Argumentation einschränken würde.

Ein Problem ist aber noch übrig: nicht alle Algorithmen können alle möglichen Eingabedaten verarbeiten! Im Gegenteil, in den allermeisten Fällen sind nur sehr, sehr spezielle Eingabedaten zugelassen. Um diesem Problem aus dem Weg zu gehen, müssten wir eigentlich den Definitionsbereich der Funktionen einschränken, was aber recht unpraktisch ist. Daher erlauben wir, dass die Funktion für den Fall, dass das übergebene Argument nicht zum Definitionsbereich gehört, eben einfach nichts liefert. Dieser undefinierte Zustand dient als Äquivalent dafür, dass der zugehörige Algorithmus nicht anhält, das entsprechende Programm also endlos weiterläuft bzw. der Rechner "abstürzt". Funktionen dieser Art nennen wir "partielle Funktionen" (weil sie nur auf einem "Teil" der natürlichen Zahlen definiert sind); im Gegensatz dazu sind "totale Funktionen" solche, deren Definitionsbereich alle natürlichen Zahlen umfasst.

Wir erhalten damit die folgende neue Definition:

Ein Algorithmus stellt die Berechnung einer partiellen Funktion f: Df => N dar, wobei Df Í N die Definitionsmenge von f ist. Dabei gilt für jedes n Î N :

   wenn n Î Df, dann liefert der Algorithmus f(n);
   wenn n Ï Df, dann terminiert der Algorithmus nicht.


Dazu sind zwei Bemerkungen zu machen:
  1. Beachten Sie, dass diese neue Definition etwas allgemeiner ist als unsere bisherige vorläufige! Die neue Definition umfasst auch solche "Algorithmen", die nach dem bisherigen Verständnis eigentlich gar keine sind, weil sie nämlich nicht terminieren (also: anhalten)! Während wir bei der vorläufigen definierenden Beschreibung gefordert hatten, dass der Algorithmus terminieren muss, ist bei der neuen Definition über die partiellen Funktionen nun auch der Fall zugelassen, dass der Algorithmus dies nicht tut. Dies stimmt mit der täglichen Programmierpraxis überein, in der es gelegentlich schon vorkommt, dass man meint, einen "Algorithmus" (nach altem Verständnis!) zu programmieren, und erst beim Probelauf bemerkt man, dass das Programm "in einer Endlosschleife hängt".

  2. Durch die obige Definition werden die Begriffe "Algorithmus" und "partielle Funktion" nicht als äquivalent ausgewiesen! Die Definition besagt nur, dass es zu jedem Algorithmus eine passende partielle Funktion gibt. Es wird hingegen nicht gesagt, ob umgekehrt auch jeder möglichen partiellen Funktion ein Algorithmus entspricht. Mithin ist die Menge der partiellen Funktionen möglicherweise größer als die der Algorithmen. Ob das so ist und was daraus folgt, müssen wir noch untersuchen.




2.2 Wie viele Algorithmen gibt es?

 Jeder Algorithmus kann in einem Programm realisiert werden. Eine Programmiersprache heißt "universell", wenn sich mit ihr alle (aus)denkbaren Algorithmen in entsprechende Programme umsetzen lassen. Eine universelle Programmiersprache muss nicht einmal besonders raffiniert oder umfangreich sein: der Sprachumfang von Pascal, Java, C oder sonst irgend einer Programmiersprache reicht allemal. Denn Sequenz, Entscheidung und Schleifen gibt es überall, dazu ein Variablen- und ein Funktionskonzept, eventuell mit der Möglichkeit der Rekursion, - das ist schon weit mehr als nötig. Um die Anzahl der möglichen Algorithmen abzuschätzen, können wir folgendermaßen vorgehen: Aus der Vielzahl der verfügbaren Programmiersprachen wählen wir "BAPL" aus, was ein Akronym ist für den neudeutschen Programm-Namen "Best Available Programming Language". Dann programmieren wir jeden denkbaren Algorithmus in BAPL. Wenn wir - Jahrhunderte später - mit dieser Arbeit fertig sind, liegen uns die Quelltexte der Programme aller denkbaren Algorithmen vor, und das dürften durchaus viele sein. In der Praxis werden wir natürlich nicht erwarten, dass es mehr als endlich viele sind, aber wie viele sind denn eigentlich theoretisch möglich? Die Antwort liefert der folgende Satz:

Es kann höchstens abzählbar viele Algorithmen geben.

Warum ist das so? Weil die Menge der Algorithmen abzählbar ist! Und glücklicherweise ist es gar nicht so schwer, dies zu zeigen: interpretieren Sie alle Bytes des jeweiligen Algorithmus-Quelltextes als (wahrscheinlich sehr große) natürliche Zahl! Dadurch wird jedem Algorithmus eindeutig eine natürliche Zahl zugeordnet, welche man seine "Gödelnummer" nennt (nach dem Mathematiker Kurt Gödel (1906-1978), der einen der tiefsinnigsten Sätze der Mathematik des 20. Jahrhunderts formuliert und bewiesen hat - dazu später mehr). Zwei verschiedene Algorithmen müssen auch zwei verschiedene Gödelnummern haben, weil gleiche Gödelnummern nur bei gleichen Quelltexten vorkommen können, und das kann ja nicht sein bei verschiedenen Algorithmen. Also kann man von einer Gödelnummer eindeutig auf den zugehörigen Algorithmus zurückschließen. Eine solche eindeutige Abbildung von Objekten auf die natürlichen Zahlen nennt man eine "Gödelisierung" dieser Objekte. Ordnet man die Algorithmen nach aufsteigenden Gödelnummern an, dann hat man eine wohlgeordnete Liste aller möglichen Algorithmen. Daraus folgt, dass es höchstens so viele (verschiedene) Algorithmen geben kann, wie es natürliche Zahlen gibt - also abzählbar viele!



Aufgaben:


  1. Ordnung muss sein...

    Jede Gödelnummer aus dem obigen Verfahren ist eine natürliche Zahl. Ist auch jede natürliche Zahl eine Gödelnummer? Begründen Sie Ihre Entscheidung!

    Denken Sie sich ein erweitertes Gödelisierungs-Verfahren aus, das zu einer wirklich bijektiven Abbildung zwischen den Algorithmen und der Menge der natürlichen Zahlen führt.
    [Lösungsvorschlag]


  2. Algorithmen nummerieren

    Schreiben Sie ein Programm, das eine beliebige Textdatei einliest, die Gödelnummer dieses Textes berechnet und diese dann in eine Datei mit dem Namen der QuellText-Datei und der Endung ".goe" schreibt.

    Kann man das Programm auch auf seinen eigenen Quelltext anwenden?
    [Lösungsvorschlag]





2.3 Kann ein Computer "alles" berechnen?

 Man könnte die Frage auch so formulieren: Gibt es zu allen partiellen Funktionen jeweils einen Algorithmus? Die Antwort darauf lautet: Nein! Wir wissen aus dem letzten Abschnitt, dass es höchstens abzählbar viele Algorithmen geben kann. Unter Mathematikern ist nun bekannt, dass es überabzählbar viele partielle Funktionen gibt. Also bleiben mehr als abzählbar viele partielle Funktionen übrig, zu denen es keinen Algorithmus gibt. Das heißt, dass die bei weitem meisten partiellen Funktionen nicht mit dem Computer berechenbar sind. Die berechenbaren Funktionen wären damit sozusagen "seltene Ereignisse"!

Wie kann man nun einsehen, dass es überabzählbar viele partielle Funktionen gibt? Wir führen einen Beweis durch Widerspruch: wir nehmen an, es gäbe nur abzählbar viele partielle Funktionen. Diese gödelisieren wir und ordnen die Funktionen dann nach der Größe der Gödelnummern in einer linearen Liste an. Nun nummerieren wir die Funktionen (und damit die möglichen Programme) neu durch, indem wir die Reihe der natürlichen Zahlen als Indizes verwenden. Wir erhalten damit eine wohlgeordnete Liste aller möglicher partieller Funktionen:
(f0, f1, f2, f3, .... , fi, .....)

Nun definieren wir eine Funktion p auf folgende Art und Weise:


Diese Funktion p muss ebenfalls in der von uns zuvor erstellten Liste vorkommen! Wir gehen die Liste durch, bis wir die Funktion gefunden haben: p = fe ! Aha, es ist also die Funktion mit dem Index e!

Die Funktion p ist im übrigen sogar eine totale Funktion, weil Sie nämlich für alle natürlichen Zahlen definiert ist. Daher sollten wir gefahrlos nach dem Wert von p(e) fragen dürfen: wegen p = fe ist natürlich p(e) = fe(e). Aber nach der obigen Definition von p erhält man p(e) = fe(e) + 1 und damit p(e) = p(e) + 1. Wie groß auch immer p(e) sein mag - dies ist ein krasser Widerspruch!

Also muss eine der Voraussetzungen falsch gewesen sein: unsere einzige Annahme war jedoch, dass es höchstens abzählbar viele partielle Funktionen geben sollte. Das ist damit offensichtlich falsch, weshalb es also überabzählbar viele partielle Funktionen geben muss. (Insbesondere kann unsere oben definierte Funktion g offenbar nicht in der Liste der "abgezählten" partiellen Funktionen vorkommen.) Damit ist aber klar, dass die meisten partiellen Funktionen nicht mit dem Computer berechenbar sind, weil dafür nicht mehr als abzählbar viele Algorithmen zur Verfügung stehen.

Und das hat nun auch wirklich nichts damit zu tun, dass die "Entwicklung der Rechner" eben noch nicht genügend weit fortgeschritten ist! Nein, es wird immer so bleiben, dass nicht alle exakt formulierbaren Probleme algorithmisch gelöst werden können, weil eben aus logischen Gründen die Reichweite des algorithmischen Verfahrens bei weitem nicht so groß ist, wie wir naiven Computeranbeter gewöhnlich glauben!



Aufgaben:


  1. Ein falscher Fehler?

    Fritzchen Pfiffig hat in obigem Beweis einen Fehler entdeckt. Seiner Meinung nach müsste bei der Berechnung von p(e) die zweite Zeile der Definition von p zum Zuge kommen, und nicht die erste. Damit wäre dann p(e) = 0. Können Sie das nachvollziehen?
    Ist damit die Aussage des zu beweisenden Satzes also doch falsch?


  2. Ein richtiger Fehler?

    Es gibt einen viel profunderen Einwand gegen die obige Argumentation als den der vorigen Aufgabe: er betrifft die Frage, ob die Funktion p denn eigentlich "wohldefiniert" sei. Überlegen Sie sich, wie ein Programm aussehen müsste, das den Gedankengang der Berechnung von p(e) nachvollzieht, und nehmen Sie dann Stellung zu der Frage, ob p denn wirklich "sauber definiert" ist.
    Welche Auswirkungen auf die Gültigkeit des obigen Beweises ergeben sich aus Ihren Überlegungen?



Wenn Sie nun durch die in den obigen Aufgaben geübte Kritik an dem vorstehenden Beweis so langsam daran zweifeln, dass es wirklich mehr als abzählbar viele partielle Funktionen gibt, dann kann ich Sie beruhigen: der Satz stimmt wirklich! Ich habe einen wahrhaft wunderbaren Beweis dafür entdeckt, aber leider ist auf dieser Seite nicht mehr genug Platz, um ihn hinzuschreiben.... ;-)



Zum vorigen Kapitel Zum Inhaltsverzeichnis Zum nächsten Kapitel